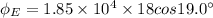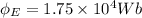Answer:
The electric flux through the car's bottom is
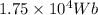
Solution:
As per the question:
Magnitude of vertical Electric field,
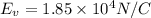
The area of the rectangular surface of the car,
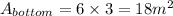
Downward slope at an angle,
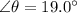
Now, the electric flux,
 is given by:
is given by:
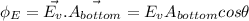
Now, substituting the appropriate values in the above formula: