Question

A car that weighs 1.0 x 10^4 N is initially moving at a speed of 38 km/h when the brakes are applied and the car is brought to a stop in 20 m. Assuming that the force that stops the car is constant, find (a) the magnitude of that force and (b) the time required for the change in speed. If the initial speed is doubled, and the car experiences the same force during the braking, by what factors are (c) the stopping distance and (d) the stopping time multiplied? (There could be a lesson here about the danger of driving at high speeds.)

Answer 1

Part a) Force on car = 2833.84 Newtons

Part b) Time to stop the car = 3.8 seconds

Part c) Factor for stopping distance is 4.

Part d) Factor for stopping time is 1.

Step-by-step explanation:

The deceleration produced when the car is brought to rest in 20 meters can be found by third equation of kinematics as

`v^2=u^2+2as`

where

v = final speed of the car ( = 0 in our case since the car stops)

u = initial speed of the car = 38 km/hr =
`(38* 1000)/(3600)=10.56m/s`

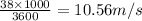
a = deceleration produces

s = distance in which the car stops

Applying the given values we get

`0^2=10.56^2+2* a* 20\\\\a=(0-10.56^2)/(2* 20)\\\\\therefore a=-2.78m/s^2`

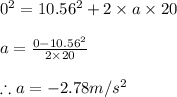
Now the force can be obtained using newton's second law as

`Force=(Weight)/(g)* a`

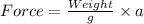
Applying values we get

`Force=(1.0* 10^4)/(9.81)* -2.78\\\\\therefore F=-2833.84Newtons`

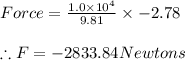
The negative direction indicates that the force is opposite to the motion of the object.

Part b)

The time required to stop the car can be found using the first equation of kinematics as

`v=u+at` with symbols having the same meanings

Applying values we get

`0=10.56-2.78* t\\\\\therefore t=(10.56)/(2.78)=3.8seconds`

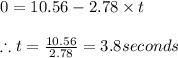
Part c)

From the developed relation of stopping distance we can see that the for same force( Same acceleration) the stopping distance is proportional to the square of the initial speed thus doubling the initial speed increases the stopping distance 4 times.

Part d)

From the relation of stopping time and the initial speed we can see that the stopping distance is proportional initial speed thus if we double the initial speed the stopping time also doubles.