Answer:
6
Explanation:
Given information:
Interior angle of a polygon cannot be more that 180°.
One interior angle =
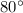
Other interior angles are =
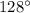
Let n be the number of sides of the polygon.
Sum of interior angles is
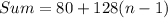
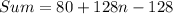
Combine like terms.
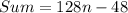 .... (1)
.... (1)
If a polygon have n sides then the sum of interior angles is
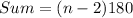
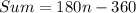 .... (2)
.... (2)
Equating (1) and (2) we get
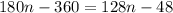
Isolate variable terms.
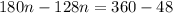
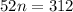
Divide both sides by 52.
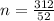
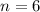
Therefore the number of sides of the polygon is 6.