Question

On a distant planet, golf is just as popular as it is on earth. A golfer tees off and drives the ball 3.00 times as far as he would have on earth, given the same initial velocities on both planets. The ball is launched at a speed of 44.4 m/s at an angle of 25° above the horizontal. When the ball lands, it is at the same level as the tee. On the distant planet, what are (a) the maximum height and (b) the range of the ball?

Answer 1

(a) Maximum height = 53.88 meters

(b) Range of the ball = 924.36 meters

Step-by-step explanation:

The ball has been launched at a speed = 44.4 meters per second

Angle of the ball with the horizontal = 25°

Horizontal component of the speed of the ball = 44.4cos25° = 40.24 meters per second

Vertical component = 44.4sin25° = 18.76 meters per second

We know vertical component of the speed decides the height of the ball so by the law of motion,

v² = u² - 2gh

where v = velocity at the maximum height = 0

u = initial velocity = 18.76 meter per second

g = gravitational force = 9.8 meter per second²

Now we plug in the values in the given equation

0 = (18.76)² - 2(9.8)(h)

19.6h = 352.10

h =
`(352.10)/(19.6)`

h = 17.96 meters

By another equation,

`v=ut-(1)/(2)gt^(2)`

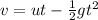
Now we plug in the values again

`0=(18.76)t-(1)/(2)(9.8)t^(2)`

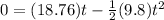
18.76t = 4.9t²

18.76 = 4.9t

t =
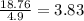`(18.76)/(4.9)=3.83`seconds

Since time t is the time to cover half of the range.

Therefore, time taken by the ball to cover the complete range = 2×3.83 = 7.66 seconds

So the range of the ball = Horizontal component of the velocity × time

= 40.24 × 7.66

= 308.12 meters

This we have calculated all for our planet.

Now we take other planet.

(a) Since the golfer drives the ball 3 times as far as he would have on earth then maximum height achieved by the ball = 17.96 × 3 = 53.88 meters

(b) Range of the ball = 3×308.12 = 924.36 meters