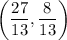Question

Gandalf the Grey started in the Forest of Mirkwood at a point P with coordinates (3, 0) and arrived in the Iron Hills at the point Q with coordinates (5, 5). If he began walking in the direction of the vector v - 3i + 2j and changes direction only once, when he turns at a right angle, what are the coordinates of the point where he makes the turn?

Answer 1

Turning point has coordinates
`\left((27)/(13),(8)/(13)\right)`

Explanation:

Gandalf the Grey started in the Forest of Mirkwood at a point P(3, 0) and began walking in the direction of the vector
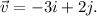`\vec{v}=-3i+2j.` The coordinates of the vector v are (-3,2). Then he changed the direction at a right angle, so he was walking in the direction of the vector
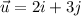`\vec{u}=2i+3j` (vectors u and v are perpendicular).

Let B(x,y) be the turning point. Find vectors PB and BQ:

`\overrightarrow{PB}=(x-3,y-0)\\ \\\overrightarrow {BQ}=(5-x,5-y)`

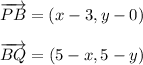
Note that vectors v and PB and vectors u and BQ are collinear, so

`(x-3)/(-3)=(y)/(2)\\ \\(5-x)/(2)=(5-y)/(3)`

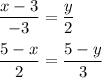
Hence

`2(x-3)=-3y\Rightarrow 2x-6=-3y\\ \\3(5-x)=2(5-y)\Rightarrow 15-3x=10-2y`

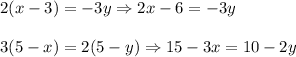
Now solve the system of two equations:

`\left\{\begin{array}{l}2x+3y=6\\ -3x+2y=-5\end{array}\right.`

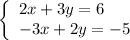
Multiply the first equation by 3, the second equation by 2 and add them:

`3(2x+3y)+2(-3x+2y)=3\cdot 6+2\cdot (-5)\\ \\6x+9y-6x+4y=18-10\\ \\13y=8\\ \\y=(8)/(13)`

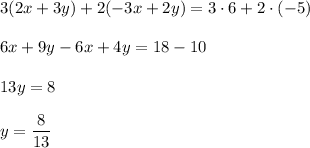
Substitute it into the first equation:

`2x+3\cdot (8)/(13)=6\\ \\2x=6-(24)/(13)=(54)/(13)\\ \\x=(27)/(13)`

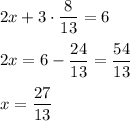
Turning point has coordinates
`\left((27)/(13),(8)/(13)\right)`