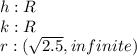Question

Find all possible circles that pass through these points: (0,2), (3,1) [Linear Algebra]

I have tried using the equation of a circle to set up an augmented matrix but I'm not sure where to go after I plug in x & y for the equation. I was told that if there is two points, then there will be infinitely many equations.

Answer 1

Infinite circles but with values (h,k,r)=(h,3h-3,√(10h²-30h+25))

Explanation:

You are correct, if we only have two points, then we will have infinite possibilities, but all those circles will have to be attached to those two points. We have to find a condition to have infinite circles which pass through those points.

Let h be the x coordinate of the center of the circle

Let k be the y coordinate of the center of the circle

Let r be the radius of the circle. Having the circle equation:

`(x-h)^(2)+(y-k)^(2)=r^(2)`

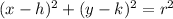
And now expand every binomial and substitute the values of the points:

`(x-h)^(2)+(y-k)^(2)=r^(2)\\\\(0-h)^(2)+(2-k)^(2)=r^(2)\\\\(3-h)^(2)+(1-k)^(2)=r^(2)`

`x^(2)-2xh+h^(2)+y^(2)-2yk+k^(2)=r^(2)\\\\h^(2)+4-4k+k^(2)=r^(2) (I)\\\\9-6h+h^(2)+1-2k+k^(2)=r^(2)`

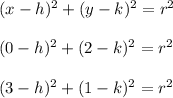
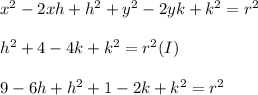
Now substract the first and secod equation, and then the first and the third one:

`x^(2)-2xh+y^(2)-4-2yk+4k=0\\\\x^(2)-9-2xh+6h+y^(2)-1-2yk+2k=0`

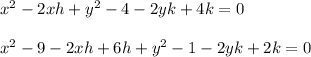
Now we substract the second equation from the first one:

`-4+4k+9-6h+1-2k=0`

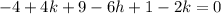
Reduce terms and we will have a linear equation, clear k:

`2k-6h+6=0\\\\k=3h-3`

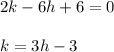
The last equation let us know the value of k if we asign any value to h.

Now we substitute h and k=3h-3 in I:

`h^(2)+4-4(3h-3)+(3h-3)^(2)=r^(2)\\\\10h^(2)-30h+25=r^(2)\\\\r=\sqrt{10h^(2)-30h+25}`

The last equation let us know the value of r if we asign any value to h.

These equations (in fact functions), will let us know every set for h, k and r to form a circle (which will pass through the mentioned points)

`(h,k,r)=(h,3h-3,\sqrt{10h^(2)-30h+25})`

Where the indepent variable is h for any real, k is any real and the minimum r is √2.5:

`h:R\\k:R\\r:(√(2.5),infinite)`