Answer:
a) The magnitude of the car's total displacement (T) from the starting point is T = 82.67 Km
b) The angle (θ) from east of the car's total displacement measured from the starting direction is θ = 40.88 °
Step-by-step explanation:
Attached you can see a diagram of the problem.
a) Find the magnitude of the vector T that goes from point A to point D (see the diagram).
The x and y components of this vector are
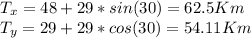
The magnitude of the vector is find using the pythagoras theorem:
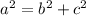 , being a, b and c the 3 sides of the triagle that forms the vector:
, being a, b and c the 3 sides of the triagle that forms the vector:

Replacing the values
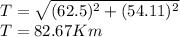
b) Find the angle θ that forms the vector T and the vector AB (see diagram).
To find this angle you can use the inverse tangent
θ
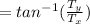
θ
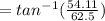
θ=40.88°