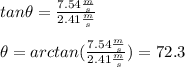Question

A diver springs upward from a board that is 3.90 m above the water. At the instant she contacts the water her speed is 11.8 m/s and her body makes an angle of 78.2° with respect to the horizontal surface of the water. Determine her initial velocity, both (a) magnitude and (b) direction.

Answer 1

V = 7.91 m/s(magnitude) @ 72.3°(direction)

Step-by-step explanation:

We will have to do a parabolic movement analysis in order to determine the initial velocity. For this we will mainly use the following kinetic formulae:

`1) X_(f)=X_(0)+V_(0)t+(at^(2))/(2)\\\\2) V_(f)=V_(0)+at`

We will work backwards from the initial information: a final velocity of 11.5 m/s at a 78.2° angle. From this we can extract the final horizontal and vertical velocity:

`V_(fx)=11.8(m)/(s)*Cos(78.2)=2.41(m)/(s)\\\\V_(fy)=11.8(m)/(s)*Sin(78.2)=11.55(m)/(s)`

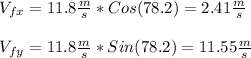
We will use
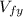`V_(fy)` with a negative value (since the diver is moving in a downwards direction). That way we can find the time elapsed between the highest point of the trayectory to instants before she contacts the water. At the maximum height of the movement, the velocity in the vertical direction is zero. Therefore we can rewrite equation 2) and solve for t:

`-11.55(m)/(s)=0(m)/(s) - 9.8(m)/(s^(2))t\\\\t= (-11.55(m)/(s))/(- 9.8(m)/(s^(2)))=1.17s`

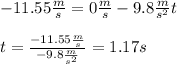
This t that we found represents the time from the maximum height to the surface of the water. Now we can use equartion 1) to determine the maximum height. We must remember a starting point of 3.9m above the water:

`0 = h+3.9m+0(m)/(s)*t-(9.8(m)/(s^(2))t^(2))/(2)\\ \\h=(9.8(m)/(s^(2))1.17s^(2))/(2)-3.9m=2.9m\\\\`

Since we now know what is the maximum height we can determine the time that it took for the diver to reach that point using equation 1) and 2):

`2.9m =V_(0y)t-(9.8(m)/(s^(2))t^(2))/(2)\\\\0(m)/(s)= V_(0y)t-9.8(m)/(s^(2))t`

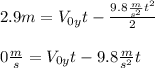
We will solve for
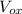`V_(ox)` in equation 2) and replace it in equation 1):

`V_(0y) = 9.8(m)/(s^(2))t\\\\2.9m =(9.8(m)/(s^(2))t)t-(9.8(m)/(s^(2))t^(2))/(2)`

We solve for t (time from diving board to maximum height):

`2.9m =(9.8(m)/(s^(2))t)t-(9.8(m)/(s^(2))t^(2))/(2)\\\\2.9m=(9.8(m)/(s^(2))t^(2))/(2)\\\\5.8m=9.8(m)/(s^(2))t^(2)\\\\t=\sqrt{ (5.8m)/(9.8(m)/(s^(2)))}=0.77s`

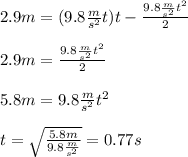
Finally we can replace our t value in
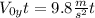`V_(0y)t=9.8(m)/(s^(2))t` to obtain:

`V_(0y)t=9.8(m)/(s^(2))t=9.8(m)/(s^(2))*0.77s=7.54(m)/(s)`

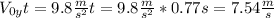
With this we have the information we need in order to determine the initial velocity of the diver. The magnitude will be calculated from the initial horizontal and vertical velocities (consider final and initial horizontal velocity to be equal in PARABOLIC MOVEMENTS):

`V_(0)=\sqrt{V_(0x)^(2)+V_(0y)^(2)}=\sqrt{(2.41(m)/(s))^(2)+(7.54(m)/(s))^(2)}=7.91(m)/(s)`

And the direction is determined by an arctangent:

`tan\theta=(7.54(m)/(s))/(2.41(m)/(s))\\\\\theta=arctan((7.54(m)/(s))/(2.41(m)/(s)))=72.3`