Question

For what value(s) of, if any, is the given vector parallel to = (4,-1)? (a) (8r,-2) (b) (8t, 21)

Answer 1

r=1 and t= -21/2.

Explanation:

Two vectors are parallel if both are multiples. That is, for a vector (x,y), the parallel vector to (x,y) will be of the form k(x,y) with k a real number. Then,

a) (8r, -2) = 2(4r,-1). Then, we need to have that r=1, in other case the first component wouldn't be 4 or the second component wouldn't be -1 and the vector (8r,-2) wouldn't be parallel to (4, -1).

b) for the case of (8t, 21) we need -1 in the second component and 4 in the first component, then let t= -21/2 to factorize the -21 and get 4 in the fisrt component and -1 in the second component.

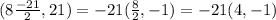`(8(-21)/(2), 21) = -21((8)/(2), -1) = -21(4,-1)`. In other case, the vector (8t, 21) wouldn't be parallel to (4,-1).