Question

A tank holds 10.3 mol of an ideal gas at an absolute pressure of 519 kPa while at a temperature of 361.38°C. (a) Compute the container's volume (b) The gas is now heated to 651.6 °C. What is the pressure of the gas now?

Answer 1

(a) 62.57 L

(b) 801.94 kPa

Step-by-step explanation:

Given:

`n` = number of moles of gas = 10.3 mol

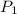`P_1` = initial pressure of the gas =
`519\ kPa = 5.19* 10^5\ Pa`

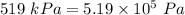
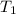`T_1` = initial temperature of the gas =
`361.38^\circ C = (361.38+273)\K = 598.38\ K`

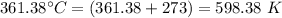
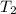`T_2` = final temperature of the gas =
`651.6^\circ C = (651.6+273)\K = 924.6\ K`

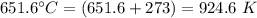
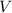`V` = volume of the tank

R = universal gas constant =
`8.314 J/mol K`

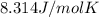
Part (a):

Using Ideal gas equation, we have

`PV=nRT\\\Rightarrow V = (nRT)/(P)\\\Rightarrow V = (10.3* 8.314* 598.38)/(5.19* 10^(5))\\\Rightarrow V = 6.2567*10^(-2)\ m^3\\\Rightarrow V = 62.567\ L`

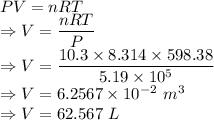
Hence, the volume of the container is 62.567 L.

Part (b):

As the volume of the container remains constant.

Again using ideal gas equation,

`PV=nRT\\\because V,\ n, R\ are\ constant\\\therefore (P_1)/(P_2)=(T_1)/(T_2)\\\Rightarrow P_2 = (T_2)/(T_1)P_1\\\Rightarrow P_2 = (924.6)/(598.38)* 519\\\Rightarrow P_2 = 801.94\ kPa`

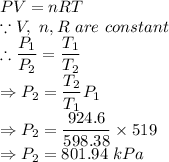
Hence, the final pressure of the gas is now 801.94 kPa.