Question

Solve the linear system by Gaussian-Jordan elimination. a) x1 + x2 + 2x3 = 8 b) x – y + 2z - w = -1 – x1 – 2x2 + 3x3 = 1 2x + y - 22 – 2w = -2 3x1 – 7x2 + 4x3 = 10 -x + 2y – 4z +w=1 3x – 3w = -3

Answer 1

Solution for the linear system:

a)
`X_1=3, X_2=1, X_3=2`

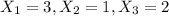
b)
`x= w-1\\y=2z`

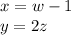
z and w are free, meaning that can have any value, for this reason, this system has infinite solutions.

Explanation:

Gaussian-Jordan elimination consists of taking an augmented matrix, and transform it into its Row echelon form by means of row operation. For notation, R_i will be the transform column, and r_i the actual one.

Linear System a)

First, you have to convert the system into matrix notation, in this case, column 1 corresponds to variable x_1, column 2 to x_2, column 3 to x_3 and column 4 to the system constants:

`\left[\begin{array}{cccc}1&1&2&8\\-1&-2&3&1\\3&-7&4&10\end{array}\right]`

• Transform to 0 every number in the rows under the first row.

Operations:

`R_2=r_1+r_2\\R_3=-3r_1+r_3`

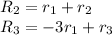
`\left[\begin{array}{cccc}1&1&2&8\\0&-1&5&9\\0&-10&-2&-14\end{array}\right]`

• Transform the -1 of the second row into 1

Operations:

`R_2=-r_2`

`\left[\begin{array}{cccc}1&1&2&8\\0&1&-5&-9\\0&-10&-2&-14\end{array}\right]`

• Transform to 0 the numbers under the 1 in the second row

Operations:

`R_3=10r_2+r_3`

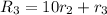
`\left[\begin{array}{cccc}1&1&2&8\\0&1&-5&-9\\0&0&-52&-104\end{array}\right]`

• Transform the -52 in the row 3 into 1

Operations:

`R_3=-(1)/(52)r_3`

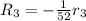
`\left[\begin{array}{cccc}1&1&2&8\\0&1&-5&-9\\0&0&1&2\end{array}\right]`

• Now write the matrix like linear equations

`x_1+x_2+2x_3=8\\x_2-5x_3=-9\\x_3=2`

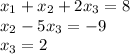
• Now that you know the valuo of x_3, you can solve the system starting from the bottom up, then find x_2 and finally x_1

`x_3=2\\x_2=-9+5*2=1\\x_1=8-1-4=3`

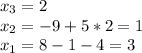
Linear System b)

For this system, the process is the same as the above.

Convert the system into matrix form

`\left[\begin{array}{ccccc}1&-1&2&-1&-1\\2&1&-2&-2&-2\\-1&2&-4&1&1\\3&0&0&-3&-3\end{array}\right]`

Operations:

`R_2=-2r_1+r_2\\R_3=r_1+r_3\\R_4=-3r_1+r_4`

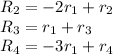
`\left[\begin{array}{ccccc}1&-1&2&-1&-1\\0&3&-6&0&0\\0&1&-2&0&0\\0&3&-6&0&0\end{array}\right]`

Operations:

`R_2=(1)/(3)r_2`

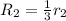
`\left[\begin{array}{ccccc}1&-1&2&-1&-1\\0&1&-2&0&0\\0&1&-2&0&0\\0&3&-6&0&0\end{array}\right]`

Operations:

`R_3=-r_2+r_3\\R_4=-3r_2+r_4`

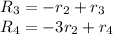
`\left[\begin{array}{ccccc}1&-1&2&-1&-1\\0&1&-2&0&0\\0&0&0&0&0\\0&0&0&0&0\end{array}\right]`

Now you can write the system as equations:

`x-y+2z-w=-1\\y-2z=0`

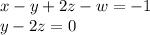
For w and z there is no unique answer, so the system result is expressed in terms of those variables. This system has infinite solutions.

Solution:

`x= w-1\\y=2z`

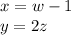
z and w are free values.