Answer:
Solution for the linear system:
a)
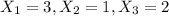
b)
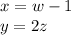
z and w are free, meaning that can have any value, for this reason, this system has infinite solutions.
Explanation:
Gaussian-Jordan elimination consists of taking an augmented matrix, and transform it into its Row echelon form by means of row operation. For notation, R_i will be the transform column, and r_i the actual one.
Linear System a)
First, you have to convert the system into matrix notation, in this case, column 1 corresponds to variable x_1, column 2 to x_2, column 3 to x_3 and column 4 to the system constants:
![\left[\begin{array}{cccc}1&1&2&8\\-1&-2&3&1\\3&-7&4&10\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/1caq61xbvnjkag60tucgyzoaihytjda7d1.png)
- Transform to 0 every number in the rows under the first row.
Operations:
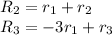
![\left[\begin{array}{cccc}1&1&2&8\\0&-1&5&9\\0&-10&-2&-14\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/jarcb1q5bj7dw0mdi4ghjddifzjdov27w0.png)
- Transform the -1 of the second row into 1
Operations:

![\left[\begin{array}{cccc}1&1&2&8\\0&1&-5&-9\\0&-10&-2&-14\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/hez5hlzajx6x6brflcuh0dd3l1drvlmjzt.png)
- Transform to 0 the numbers under the 1 in the second row
Operations:
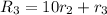
![\left[\begin{array}{cccc}1&1&2&8\\0&1&-5&-9\\0&0&-52&-104\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/h7gbwp329itfzyh51ngkksodl4z24rdqsd.png)
- Transform the -52 in the row 3 into 1
Operations:
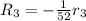
![\left[\begin{array}{cccc}1&1&2&8\\0&1&-5&-9\\0&0&1&2\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/cossdt6ya5l419nfbw69yf4dc2frhmp3m7.png)
- Now write the matrix like linear equations
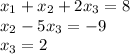
- Now that you know the valuo of x_3, you can solve the system starting from the bottom up, then find x_2 and finally x_1
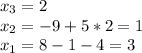
Linear System b)
For this system, the process is the same as the above.
Convert the system into matrix form
![\left[\begin{array}{ccccc}1&-1&2&-1&-1\\2&1&-2&-2&-2\\-1&2&-4&1&1\\3&0&0&-3&-3\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/zgtduhoak3zzuuj4k4sqn8blvwjpo3kaux.png)
Operations:
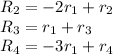
![\left[\begin{array}{ccccc}1&-1&2&-1&-1\\0&3&-6&0&0\\0&1&-2&0&0\\0&3&-6&0&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/jd25l39kjlv3gbxx7lrzdkd9w25xgo70v7.png)
Operations:
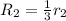
![\left[\begin{array}{ccccc}1&-1&2&-1&-1\\0&1&-2&0&0\\0&1&-2&0&0\\0&3&-6&0&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/ispxcpxwtdn869cjh8hr7ppkujv99ykrwy.png)
Operations:
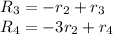
![\left[\begin{array}{ccccc}1&-1&2&-1&-1\\0&1&-2&0&0\\0&0&0&0&0\\0&0&0&0&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/4icfkyg5ayballjn6d9jr05tg4l09h446z.png)
Now you can write the system as equations:
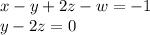
For w and z there is no unique answer, so the system result is expressed in terms of those variables. This system has infinite solutions.
Solution:
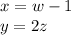
z and w are free values.