Question

Find the optimal solution for the following problem

Minimize C = 13x + 3y
subject to 12x + 14y ≥ 21
15x + 20y ≥ 37
and x ≥ 0, y ≥ 0.
1. What is the optimal value of x?

2. What is the optimal value of y?

3.What is the minimum value of the objective function?

Answer 1

Minimize C =
`13x + 3y`

`12x + 14y \geq  21`

`15x + 20y \geq 37`

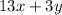
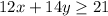
and x ≥ 0, y ≥ 0.

Plot the the lines on the graph and find the feasible region

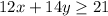`12x + 14y \geq  21` -- Blue

`15x + 20y \geq  37` --- Green

So, the boundary points of feasible region are (-3.267,4.3) , (0,1.85) and (2.467,0)

Substitute the value in Minimize C

Minimize C =
`13x + 3y`

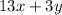
At (-3.267,4.3)

Minimize C =
`13(-3.267) + 3(4.3)`

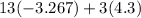
Minimize C =
`-29.571`

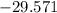
At (0,1.85)

Minimize C =
`13(0) + 3(1.85)`

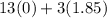
Minimize C =
`5.55`

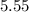
At (2.467,0)

Minimize C =
`13(2.467) + 3(0)`

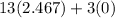
Minimize C =
`32.071`

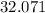
So, the optimal value of x is -3.267

So, the optimal value of y is 4.3

So, the minimum value of the objective function is -29.571