Question

The position of a particle in millimeters is given by s = 133 - 26t + t2 where t is in seconds. Plot the s-t and v-t relationships for the first 19 seconds. Determine the net displacement As during that interval and the total distance D traveled. By inspection of the s-t relationship, what conclusion can you reach regarding the acceleration?

Answer 1

Answer with Explanation:

The position of the particle as a function of time is given by
`s(t)=t^2-26t+133`

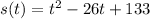
Part 1) The position as a function of time is shown in the below attached figure.

Part 2) By the definition of velocity we have

`v=(ds)/(dt)\\\\\therefore v(t)=(d)/(dt)\cdot (t^2-26t+133)\\\\v(t)=2t-26`

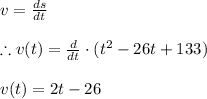
The velocity as a function of time is shown in the below attached figure.

Part 3) The displacement of the particle in the first 19 seconds is given by
`\Delta x=s(19)-s(0)\\\\\Delta x=(19^2-26* 19+133)-(0-0+133)=-133millimeters`

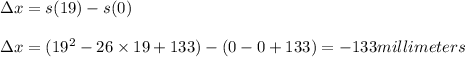
Part 4) The distance covered in the first 19 seconds can be found by evaluating the integral

`s=\int _(0)^(19)\sqrt{1+((ds)/(dt))^2}\\\\s=\int _(0)^(19)√(1+(2t-26)^2)\\\\\therefore s=207.03meters`

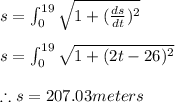
Part 4) As we can see that the position-time graph is parabolic in shape hence we conclude that the motion is uniformly accelerated motion.