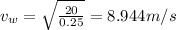Question

A 100 meter rope is 20 kg and is stretched with a tension of 20 newtons. If one end of the rope is vibrated with small amplitude at 10Hz, what would the velocity of waves traveling down it be? What would the velocity be if it rained and the rope soaked up 5 kg of water?

Answer 1

The velocity waves before rain is 10 m/s

The velocity of wave after the rope soaked up 5 kg more is 8.944 m/s

Solution:

As per the question:

Length of the rope, l = 100 m

Mass of the rope, m = 20 kg

Force due to tension in the rope,
`T_(r) = 20 N`

Frequency of vibration in the rope, f = 10 Hz

Extra mass of the rope after being soaked in rain water, m' = 5 kg

Now,

In a rope, the wave velocity is given by:

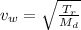`v_(w) = \sqrt{(T_(r))/(M_(d))}` (1)

where

`M_(d)` = mass density

Mass density before soaking,
`M_(d) = (m)/(l) = (20)/(100) = 0.20`

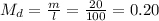
Mass density after being soaked,
`M_(d) = (m + m')/(l) = (25)/(100) = 0.25`

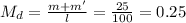
Initially, the velocity is given by using eqn (1):

`v_(w) = \sqrt{(20)/(0.20)} = 10 m/s`

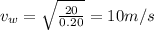
The velocity after being soaked in rain:

`v_(w) = \sqrt{(20)/(0.25)} = 8.944 m/s`