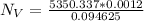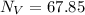Question

In American football, the playing field is 53.33 yards (yd) wide by 120 yards (yd) long. For a special game, the field staff want to paint the playing field orange. Of course, they will use biodegradable paint available for purchase in 25-gallon (gal) containers. If the paint is applied in a thickness of 1.2 millimeters (mm) in a uniform layer, how many containers of paint will they need to purchase?

Answer 1

214

Explanation:

The playing field is 53.33 yards wide and 120 yards long you would need to find the area so multiply 53.33 by 120 yards. That equals 6399.6 , the thickness they are applying is 1.2 millimeters. You would divide the area, 6399.6 by 1.2 which would equal 5333. Divide that by 25 gallons and it equals 213.32, you would need to purchase 214, rounded.

Answer 2

The number of containers to purchase is
`N_V= 67.85`

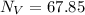
Explanation:

From the question we are told that

The playing field width is
`w_f = 53.33 \ yard = 53.33*0.9144 = 48.76m`

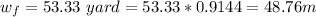
The playing field length is
`l_f = 120 \ yards = 120 * 0.9144 = 109.728m`

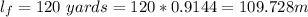
The volume of one container is
`V= 25 \ gallon = 25 * 0.00378541 = 0.094625m^3`

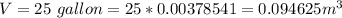
The thickness of the painting is
`t = 1.2 \ mm = 1.2 * 0.001 = 0.0012m`

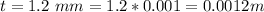
The area of the playing field is
`A = 48.76 * 109.728`

`=5350.337m^2`

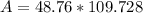
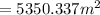
The number of container of paint needed
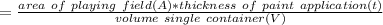
`N_V`
`= (area \ of \ playing \ field(A) * thickness \ of \ paint \ application(t) )/(volume\ single \ container(V))`

=>
`N_V = (5350.337 * 0.0012)/(0.094625)`

`N_V= 67.85`