Question

If 4 divides a^2-3b^2, then at least one of the integers a and b is even.

Answer 1

Explanation:

The proof can be done by contradiction. Suppose both a, and b weren't even. So that a, and b are both odd. This means they both look like

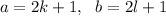`a=2k+1,~~b=2l+1` (for some integers k and l)

So, let's compute what
`a^2-3b^2` would be in this case:

`a^2-3b^2=(2k+1)^2-3(2l+1)^2=4k^2+4k+1-3(4l^2+4l+1)`

`= 4k^2+4k+1-12l^2-12l-3=4k^2+4k-12l^2-12l-2`

`=4(k^2+k+3l^2-3l)-2`

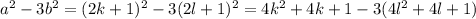
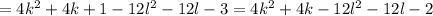
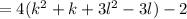
which notice wouldn't be divisible by 4. This shows then that since
`a^2-3b^2` is divisible by 4, at least one of the integers a and b is even.