Answer:
 is a factor of
is a factor of
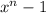
Step-by-step explanation:
 is a factor of
is a factor of
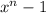
We will prove this with the help of principal of mathematical induction.
For n = 1,
 is a factor
is a factor
 , which is true.
, which is true.
Let the given statement be true for n = k that is
 is a factor of
is a factor of
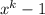 .
.
Thus,
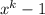 can be written equal to
can be written equal to
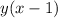 , where y is an integer.
, where y is an integer.
Now, we will prove that the given statement is true for n = k+1
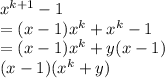
Thus,
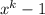 is divisible by
is divisible by
 .
.
Hence, by principle of mathematical induction, the given statement is true for all natural numbers,n.