Question

Pigeon Hole Principle :

Prove that given any set of n + 1 integers, there must be at least one pair among them whose difference is divisible by n

Answer 1

Explanation:

When you divide an integer number by n, you get a remainder of either 0, 1, 2, ..., n-1 (for example 5 divided by 2 leaves a remainder of 1, or 13 divided by 5 leaves a remainder of 3, or 16 divided by 2 leaves a remainder of 0, and so on).

So there are n different remainders we could get when dividing an integer number by n. If we are given n+1 numbers, they each leave a certain remainder when divided by n. Since there are only n possible remainders, and we have n+1 numbers, by the pigeonhole principle we know there must be at least 2 numbers that leave the same remainder when divided by n. Call them numbers a and b, and let's call r the remainder they leave when divided by n. So both a and b are of the form:

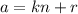`a=kn+r` (for some integer k)

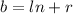`b=ln+r` (for some integer l)

(this is exactly what it means to leave a remainder of r when divided by n)

And so their difference is

`a-b=kn+r-(ln+r)=kn-ln=(k-l)n`

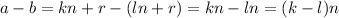
Which is divisible by n by definition of being divisible (or think of it as a-b being a multiple of n, so it's divisible by n).