Answer:
(a). The car's total displacement from its starting point is 76.58 m.
(b). The angle of the car's total displacement measured from its starting direction is 36.81°.
Step-by-step explanation:
Given that,
Distance = 47 km in east
Distance = 23 km in north
Angle = 32° east of north
Distance = 27 km
According to figure,
Angle = 90-32 = 58°
(a). We need to calculate the magnitude of the car's total displacement from its starting point
Using Pythagorean theorem

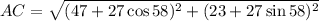
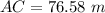
The magnitude of the car's total displacement from its starting point is 76.58 m.
(b). We need to calculate the angle (from east) of the car's total displacement measured from its starting direction
Using formula of angle
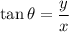
put the value into the formula
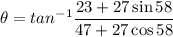
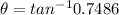

Hence, (a). The car's total displacement from its starting point is 76.58 m.
(b). The angle of the car's total displacement measured from its starting direction is 36.81°.