Question

Find the reduced row echelon form of the following matrices and then give the solution to the system that is represented by the augmented matrix. TO 4 7 0 6. a. 2 1 0 0 Lo 3 1 - 4 6. b. 54 30 71 8 6 2 -3 4 3 2 -10]

Answer 1

a)

Reduced Row Echelon:

`\left[\begin{array}{cccc}1&1/2&0&0\\0&1&7/4&0\\0&0&1&-4\end{array}\right]`

Solution to the system:

`x_3=-4\\x_2=-(7)/(4)x_3=7\\x_1=-(1)/(2)x_2=-(7)/(2)`

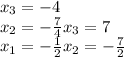
b)

Reduced Row Echelon:

`\left[\begin{array}{cccc}4&3&0&7\\0&0&2&-17\\0&0&2&-17\end{array}\right]`

Solution to the system:

`x_3=-(17)/(2)\\x_1=(7-3x_2)/(4)`

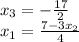
x_2 is a free variable, meaning that it has infinite possibilities and therefore the system has infinite number of solutions.

Explanation:

To find the reduced row echelon form of the matrices, let's use the Gaussian-Jordan elimination process, which consists of taking the matrix and performing a series of row operations. For notation, R_i will be the transformed column, and r_i the unchanged one.

a)
`\left[\begin{array}{cccc}0&4&7&0\\2&1&0&0\\0&3&1&-4\end{array}\right]`

Step by step operations:

1. Reorder the rows, interchange Row 1 with Row 2, then apply the next operations on the new rows:

`R_1=(1)/(2)r_1\\R_2=(1)/(4)r_2`

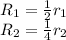
Resulting matrix:

`\left[\begin{array}{cccc}1&1/2&0&0\\0&1&7/4&0\\0&3&1&-4\end{array}\right]`

2. Set the first row to 1

`R_3=-3r_2+r_3`

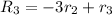
Resulting matrix:

`\left[\begin{array}{cccc}1&1/2&0&0\\0&1&7/4&0\\0&0&1&-4\end{array}\right]`

3. Write the system of equations:

`x_1+(1)/(2)x_2=0\\x_2+(7)/(4)x_3=0\\x_3=-4`

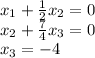
Now you have the reduced row echelon matrix and can solve the equations, bottom to top, x_1 is column 1, x_2 column 2 and x_3 column 3:

`x_3=-4\\x_2=-(7)/(4)x_3=7\\x_1=-(1)/(2)x_2=-(7)/(2)`

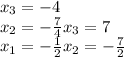
b)

`\left[\begin{array}{cccc}4&3&0&7\\8&6&2&-3\\4&3&2&-10\end{array}\right]`

1.
`R_2=-2r_1+r_2\\R_3=-r_1+r_3`

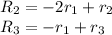
Resulting matrix:

`\left[\begin{array}{cccc}4&3&0&7\\0&0&2&-17\\0&0&2&-17\end{array}\right]`

2. Write the system of equations:

`4x_1+3x_2=7\\2x_3=-17`

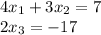
Now you have the reduced row echelon matrix and can solve the equations, bottom to top, x_1 is column 1, x_2 column 2 and x_3 column 3:

`x_3=-(17)/(2)\\x_1=(7-3x_2)/(4)`

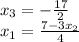
x_2 is a free variable, meaning that it has infinite possibilities and therefore the system has infinite number of solutions.