Question

Provide a beautiful proof of the following claim: The square of a rational number is a rational number.

Answer 1

Square of a rational number is a rational number.

Explanation:

Let m be a rational number. Thus, m can be written in the form of fraction
`(x)/(y)`, where x and y are integers and
`y \\eq 0`.

The square of m =
`m* m = m^2`

`m^2 = (x)/(y) *(x)/(y) = (x^2)/(y^2)`

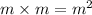
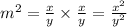
It is clearly seen, that
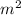`m^2`, can be easily written in the form of fraction and the denominator is not equal to zero.

Hence,
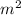`m^2` is a rational number.

This can also be understood with the help of the fact that rational numbers are closed under multiplication that is product of a rational number is also a rational number.