Answer:
R is reflexive
R is not symmetric
R is transitive
Explanation:
R is reflexive.
To show this, we have to verify that for any pair of integers
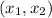
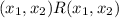 .
.
But this is obvious because
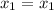 and
and
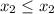 .
.
R is not symmetric.
To show it, we need to find two pairs
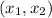 and
and
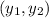 such that
such that
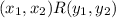
but
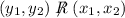
For example (1,1) and (1,2).
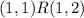 for 1=1 and
for 1=1 and
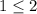 but
but
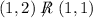 because
because
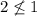
Finally, R is transitive.
If we take 3 pairs of integers
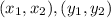 and
and
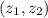
Such that
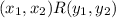 and
and
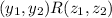 then
then
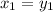 and
and
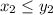
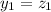 and
and
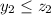
But then,
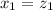 and
and

So
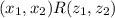 .
.