Question

A +17 nC point charge is placed at the origin, and a +8 nC charge is placed on the x axis at x=5m. At what position on the x axis is the net electric field zero? (Be careful to keep track of the direction of the electric field of each particle.) (Please explain how to do the problem.)

Answer 1

2.97m

Step-by-step explanation:

Hi!

To solve this problem we must consider the directions of the electric fields, since both charges are positive each field will point outwards form the sources meaning that the field will point yo the -x direction formpoints along the x-axis to the left of the charges and the field will point to the +x direction for points along the x-axis to the rigth of the sources, having said this, the only place where the fields point to oposite ditections is between them:

In the following diagram X is the 17nC charge and O the 8nC charge, the arrows represent the direction of their respective electric fields and d is an arbitrary distance measured from the origin.

|-------d------|-----5-d------|

X-----------> | <------------O

|---------------5--------------|

At d the electric fields of the charges are:

`E_(X)=k(17nC)/(d^(2)) \\E_(O)=-k(8nC)/((5-d)^(2))`

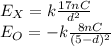
And the total field is the sum of both. Since we are looking for a position d at which the total or net electric field is zero we must solve the following equation:

`0=k((17)/(d^(2)) - (8)/((5-d)^2) )`

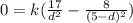
Reorganizing terms:

17*(5-d)^2-8*d^2=0

17*25-170d+9d^2=0

Solving for d, we find two solutions

d1 = 2.9655 d2=15.923

The second solution implies a distance outside the region between the charges for which the equations are no longer valid, since the direction of the 8nC field would be wrong.

So the solution is

d=2.97 m