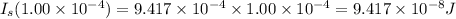Answer:
Sound Intensity at microphone's position is
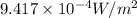
The amount of energy impinging on the microphone is
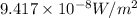
Solution:
As per the question:
Emitted Sound Power,
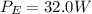
Area of the microphone,
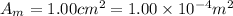
Distance of microphone from the speaker, d = 52.0 m
Now, the intensity of sound,
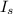 at a distance away from the souce of sound follows law of inverse square and is given as:
at a distance away from the souce of sound follows law of inverse square and is given as:
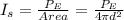
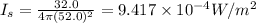
Now, the amount of sound energy impinging on the microphone is calculated as:
If
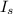 be the Incident Energy/
be the Incident Energy/
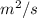
Then
The amount of energy incident per 1.00
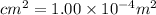 is:
is: