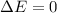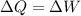Answer:
- The work made by the gas is 7475.69 joules
- The heat absorbed is 7475.69 joules
Step-by-step explanation:
Work
We know that the differential work made by the gas its defined as:
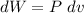
We can solve this by integration:
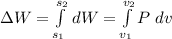
but, first, we need to find the dependence of Pressure with Volume. For this, we can use the ideal gas law
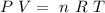
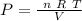
This give us
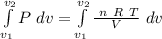
As n, R and T are constants
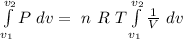
![\Delta W= \ n \ R \ T \left [ ln (V) \right ]^(v_2)_(v_1)](https://img.qammunity.org/2020/formulas/physics/college/65vb4woyxtjo63sbfujl60yv9x4f37yz4b.png)
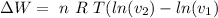
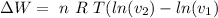
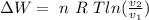
But the volume is:
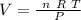
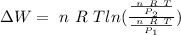
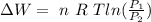
Now, lets use the value from the problem.
The temperature its:
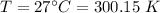
The ideal gas constant:
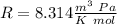
So:
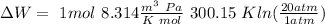
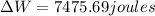
Heat
We know that, for an ideal gas, the energy is:
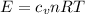
where
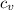 its the internal energy of the gas. As the temperature its constant, we know that the gas must have the energy is constant.
its the internal energy of the gas. As the temperature its constant, we know that the gas must have the energy is constant.
By the first law of thermodynamics, we know
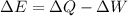
where
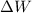 is the Work made by the gas (please, be careful with this sign convention, its not always the same.)
is the Work made by the gas (please, be careful with this sign convention, its not always the same.)
So: