Question

Consider the titration of 100 mL of 0.200 M HCHO, with 1.00 M NaOH. The pK, of HCHO2 is 3.75. a) What is the pH before ANY NaOH is added? b) What is the pH after 5.00 mL of NaOH are added? c) After 10 mL of NaOH are added? d) What is the pH when 20 mL of NaOH have been added? What is this point in the titration called?

Answer 1

a) pH = 2,23

b) pH = 3,26

c) pH = 3,74

d) pH = 7,98. Here we have the equivalence point of the titration

Step-by-step explanation:

In a titration of a strong base (NaOH) with a weak acid (HCOOH) the reaction is:

HCOOH + NaOH → HCOONa + H₂O

a) Here you have just HCOOH, thus:

HCOOH ⇄ HCOO⁻ + H⁺ where ka =1,8x10⁻⁴ and pka = 3,74

When this reaction is in equilibrium:

[HCOOH] = 0,200 -x

[HCOO⁻] = x

[H⁺] = x

Thus, equilibrium equation is:

1,8x10⁻⁴ =
`([x][x] )/([0,200-x])`

The equation you will obtain is:

x² + 1,8x10⁻⁴x - 3,6x10⁻⁵ = 0

Solving:

x = -0,006090675 ⇒ No physical sense. There are not negative concentrations

x = 0,005910674

As x = [H⁺] and pH = - log [H⁺]

pH = 2,23

b) Here, it is possible to use:

HCOOH + NaOH → HCOONa + H₂O

With adition of 5,00 mL of 1,00M NaOH solution the initial moles are:

HCOOH =
`0,100 L.(0,200 mol)/(L) =` = 2,0x10⁻² mol

NaOH =
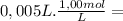`0,005 L.(1,00 mol)/(L) =` = 5,0x10⁻³ mol

HCOO⁻ = 0.

In equilibrium:

HCOOH = 2,0x10⁻² mol - 5,0x10⁻³ mol = 1,5x10⁻² mol

NaOH = 0 mol

HCOO⁻ = 5,0x10⁻³ mol

Now, you can use Henderson–Hasselbalch equation:

pH = 3,74 + log
`(5,0x10^(-3) )/(1,5x10^(-2) )`

pH = 3,26

c) With adition of 10 mL of 1,00M NaOH solution the initial moles are:

HCOOH =
`0,100 L.(0,200 mol)/(L) =` = 2,0x10⁻² mol

NaOH =
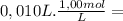`0,010 L.(1,00 mol)/(L) =` = 1,0x10⁻² mol

HCOO⁻ = 0.

In equilibrium:

HCOOH = 2,0x10⁻² mol - 1,0x10⁻² mol = 1,0x10⁻² mol

NaOH = 0 mol

HCOO⁻ = 1,0x10⁻² mol

Now, you can use Henderson–Hasselbalch equation:

pH = 3,74 + log
`(1,0x10^(-2) )/(1,0x10^(-2) )`

pH = 3,74

d) With adition of 20 mL of 1,00M NaOH solution the initial moles are:

HCOOH =
`0,100 L.(0,200 mol)/(L) =` = 2,0x10⁻² mol

NaOH =
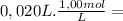`0,020 L.(1,00 mol)/(L) =` = 2,0x10⁻² mol

HCOO⁻ = 0.

Here we have the equivalence point of the titration, thus, the equilibrium is:

HCOO⁻ + H₂O ⇄ HCOOH + OH⁻ kb = kw/ka where kw is equilibrium constant of water = 1,0x10⁻¹⁴; kb = 5,56x10⁻¹¹

Concentrations is equilibrium are:

[HCOOH] = x

[HCOO⁻] = 0,1667-x

[OH⁻] = x

Thus, equilibrium equation is:

5,56x10⁻¹¹ =
`([x][x] )/([0,01667-x])`

The equation you will obtain is:

x² + 5,56x10⁻¹¹x - 9,27x10⁻¹³ = 0

Solving:

x = -9,628361x10⁻⁷⇒ No physical sense. There are not negative concentrations

x = 9,627806x10⁻⁷

As x = [OH⁻] and pOH = - log [OH⁻]; pH = 14 - pOH

pOH = 6,02

pH = 7,98

I hope it helps!