Question

While standing at the edge of the roof of a building, a man throws a stone upward with an initial speed of 7.61 m/s. The stone subsequently falls to the ground, which is 18.1 m below the point where the stone leaves his hand. At what speed does the stone impact the ground? Ignore air resistance and use g=9.81 m/s^2 for the acceleration due to gravity.

Answer 1

V=20.35m/s

Step-by-step explanation:

First of all we need to calculate the time it took the stone to reach ground level. We know that ΔY = -18.1m; Vo = 7.61m/s; g=9.81m/s2

`\Delta Y = Vo*t - g*(t^(2))/(2)`

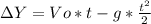
`-18.1=7.61*t-(9.81*t^(2))/(2)` Solving for t, we get:

t1 = -1.3s t2 = 2.85s We discard the negative solution and use the positive one. With this value we calculate the final velocity as:

Vf = Vo - g*t = 7.61 - 9.81 * 2.85 = -20.35 m/s

The speed is the module of the velocity, so:

V = 20.35 m/s