Question

The demand equation for kitchen ovens is given by the equation

D(q) = –338q + 4,634
where D(q) is the price in dollars and q is the number of kitchen ovens demanded per week. The supply equation for kitchen ovens is
S(q) = 400q^2 + 20
where q is the quantity the supplier will make available per week in the market when the price is p dollars. Find the equilibrium point (q, p) rounded to the nearest hundredth.

Answer 1

The equilibrium point is (3, 3620)

Explanation:

We set the supply and the demand equation equal to each other and solve:

`-338q+4634=400q^2+20\\400q^2+338q-4614=0`

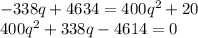
We can solve by factoring:

`2(q-3)(200q+769)=0`

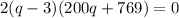
Setting each factor equal to zero we get:

`q=3\text{ or }q=\displaystyle-(769)/(200)`

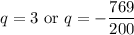
Only a positive quantity makes sense, so q=3 is the equilibrium quantity.

To get the equilibrium price we just plug 3 in place of q in any of the functions. Let us use the demand function which is easier to handle:

`D(3)=-338(3)+4634=3620`

Therefore the equilibrium price is p=3620

In ordered pair form the equilibrium point is (3, 3620)