Question

A car and a motorcycle start from rest at the same time on a straight track, but the motorcycle is 25.0 m behind the car. The car accelerates at a uniform rate of 3.70 m/s^2 and the motorcycle at a uniform rate of 4.40 m/s^2. How much time elapses before the MC overtakes the car? How far will each have traveled during that time?

Answer 1

t = 8.45 sec

car distance d = 132.09 m

bike distance d = 157.08 m

Step-by-step explanation:

GIVEN :

motorcycle is 25 m behind the car , therefore distance need to covered by bike to overtake car is 25+ d, when car reache distance d at time t

for car

by equation of motion

`d  = ut + (1)/(2)at^2`

u = 0 starting from rest

`d = (1)/(2)at^2`

`t^2 = (2d)/(a)`

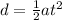
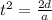
for bike

`d+25 = 0 + (1)/(2)*4.40t^2`

`t^2= (d+25)/(2.20)`

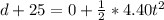
equating time of both

`(2d)/(a) = (d+25)/(2.20)`

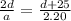
solving for d we get

d = 132 m

therefore t is
`= \sqrt{(2d)/(a)}`

`t =  \sqrt{(2*132)/(3.70)}`

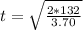
t = 8.45 sec

each travelled in time 8.45 sec as

for car

`d = (1)/(2)*3.70 *8.45^2`

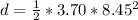
d = 132.09 m

fro bike

`d = (1)/(2)*4.40 *8.45^2`

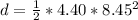
d = 157.08 m