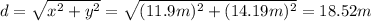Question

You kick a soccer ball at vo = 7 m/s horizontally off of the top of the Great Pyramid of Giza. The faces are slanted 40 degrees from the vertical. How far down the pyramid face does the ball hit the pyramid?

Answer 1

The ball hit the pyramid 18.52m down the pyramid face.

Step-by-step explanation:

As you can see in the image below, the will hit the pyramid at at point where the distance travelled vertically divided by the distance travelled horizontally is equal to tan(50), since it's at this moment where the path of the ball will coincide with the walls of the pyramid.

The horizontal vellocity of the ball will remain constant at a value of 7m/s along the whole journey. This is because there is no horizontal acceleration that can affect the horizontal velocity. On the contrary, the vertical velocity will start at 0m/s and will increase because of gravity.

The distance travelled horizontally will be:

`x = v_x*t = 7t`

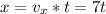
The distance travelled vertically will be:

`y = (1)/(2)gt^2+v_o_yt+y_o | v_o_y = 0m/s, y_o=0m\\ y = (1)/(2)gt^2`

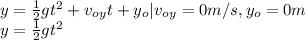
So, then:

`(y)/(x) = tan(50)\\((1)/(2)gt^2)/(v_xt) =tan(50)\\(1)/(2)gt = v_xtan(50)\\t= (2v_xtan(50))/(g) = (2*7m/s*tan(50))/(9.81m/s^2)=1.7s`

At time = 1.7s:

`x = v_x*t = 7t = 7m/s*1.7s = 11.9m`

`y=(1)/(2)gt^2 =(1)/(2)*9.81m/s^2*(1.7s)^2=14.19m`

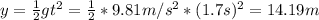
Using Pythagorean theorem, we can find the distance:

`d = √(x^2+y^2)=√((11.9m)^2+(14.19m)^2) = 18.52m`