Question

A company’s total revenue from manufacturing and selling x units of their product is given by: y = –3x2 + 900x – 5,000. How many units should be sold in order to maximize revenue, and what is the maximum revenue

Answer 1

150 units;

Maximum revenue: $62,500.

Explanation:

We have been given that a company’s total revenue from manufacturing and selling x units of their product is given by
`y=-3x^2+900x-5,000`. We are asked to find the number of units sold that will maximize the revenue.

We can see that our given equation in a downward opening parabola as leading coefficient is negative.

We also know that maximum point of a downward opening parabola is ts vertex.

To find the number of units sold to maximize the revenue, we need to figure our x-coordinate of vertex.

We will use formula
`(-b)/(2a)` to find x-coordinate of vertex.

`(-900)/(2(-3))`

`(-900)/(-6)`

`150`

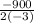
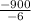
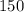
Therefore, 150 units should be sold in order to maximize revenue.

To find the maximum revenue, we will substitute
`x=150` in our given formula.

`y=-3(150)^2+900(150)-5,000`

`y=-3*22,500+135,000-5,000`

`y=-67,500+135,000-5,000`

`y=62,500`

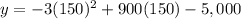
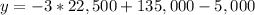
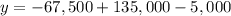
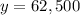
Therefore, the maximum revenue would be $62,500.