Question

A hollow sphere of inner radius 8.82 cm and outer radius 9.91 cm floats half-submerged in a liquid of density 948.00 kg/m^3. (a) What is the mass of the sphere? (b) Calculate the density of the material of which the sphere is made.

Answer 1

a) 0.568 kg

b) 474 kg/m³

Step-by-step explanation:

Given:

Inner radius = 8.82 cm = 0.0882 m

Outer radius = 9.91 cm = 0.0991 m

Density of the liquid = 948.00 Kg/m³

a) The volume of the sphere =
`(4\pi)/(3)*(0.0991^2-0.0882^2)`

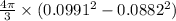
or

volume of sphere = 0.0012 m³

also, volume of half sphere =
`\frac{\textup{Total volume}}{\textup{2}}`

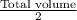
or

volume of half sphere =
`\frac{\textup{0.0012}}{\textup{2}}`

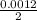
or

Volume of half sphere =0.0006 m³

Now, from the Archimedes principle

Mass of the sphere = Weight of the volume of object submerged

or

Mass of the sphere = 0.0006× 948.00 = 0.568 kg

b) Now, density =
`\frac{\textup{Mass}}{\textup{Volume}}`

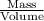
or

Density =
`\frac{\textup{0.568}}{\textup{0.0012}}`

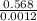
or

Density = 474 kg/m³