Question

Electric fields are vector quantities whose magnitudes are measured in units of volts/meter (V/m). Find the resultant electric field when there are two fields, E1and E2, where E1 is directed vertically upward and has magnitude 100 V/m and E2 is directed 45 degrees to the left of E1 and has magnitude 150 V/m. Use a graph to show vector drawing!

Answer 1

Er = 231.76 V/m, 27.23° to the left of E1

Step-by-step explanation:

To find the resultant electric field, you can use the component method. Where you add the respective x-component and y-component of each vector:

E1:

`E_1_x = 0V/m\\E_1_y=100V/m`

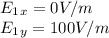
E2:

Keep in mind that the x component of electric field E2 is directed to the left.

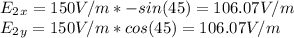
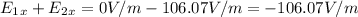
`E_2_x= 150V/m*-sin(45) = 106.07 V/m\\E_2_y=150V/m*cos(45) = 106.07V/m`

∑x:
`E_1_x+E_2_x = 0V/m - 106.07V/m = -106.07V/m`

∑y:
`E_1_y + E_2_y = 100V/m + 106.07V/m = 206.07V/m`

The magnitud of the resulting electric field can be found using pythagorean theorem. For the direction, we will use trigonometry.

`||E_r||= √((-106.07V/m)^2+(206.07V/m)^2) = 231.76 V/m\\\\\alpha = arctan((206.7 V/m)/(-106.07 V/m)) = 117.24degrees`

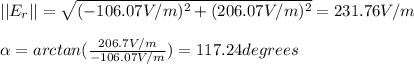
or 27.23° to the left of E1.