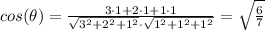Answer:
The angle between the lines
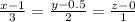 and
and
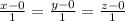 is
is
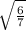
Explanation:
The equation of a line with direction vector
 that passes through the point
that passes through the point
 is given by the formula
is given by the formula
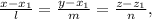 where l,m, and n are non-zero real numbers.
where l,m, and n are non-zero real numbers.
This is called the symmetric equations of the line.
The angle between two lines
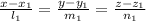 and
and
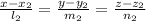 equal the angle subtended by direction vectors,
equal the angle subtended by direction vectors,
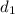 and
and
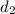 of the lines
of the lines
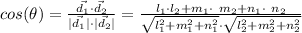
Given that
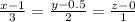 and
and
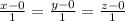
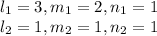
We can use the formula above to find the cosine of the angle between the lines