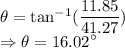Question

Suppose you walk 11 m in a direction exactly 24° south of west then you walk 21 m in a direction exactly 39° west of north. 1) How far are you from your starting point, in meters?

2) What is the angle of the compass direction of a line connecting your starting point to your final position measured North of West in degrees?

Answer 1

(1) 42.94 m

(2)
`16.02^\circ`

Step-by-step explanation:

Let us first draw a figure, for the given question as below:

In the figure, we assume that the person starts walking from point A to travel 11 m exactly
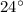`24^\circ` south of west to point B and from there, it walks 21 m exactly
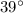`39^\circ` west of north to reach point C.

Let us first write the two displacements in the vector form:

`\vec{AB} = (-11\cos 24^\circ\ \hat{i}-11\sin 24^\circ\ \hat{j})\ m =(-10.05\ \hat{i}-4.47\ \hat{j})\ m\\\vec{BC} = (-21\sin 39^\circ\ \hat{i}+21\cos 39^\circ\ \hat{j})\ m =(-31.22\ \hat{i}+16.32\ \hat{j})\ m`

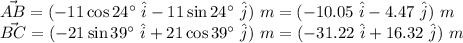
Now, the vector sum of both these vectors will give us displacement vector from point A to point C.

`\vec{AC}=\vec{AB}+\vec{BC}\\\Rightarrow \vec{AC}=(-10.05\ \hat{i}-4.47\ \hat{j})\ m+(-31.22\ \hat{i}+16.32\ \hat{j})\ m\\\Rightarrow \vec{AC}=(-41.25\ \hat{i}+11.85\ \hat{j})\ m`

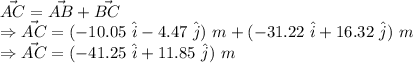
Part (1):

the magnitude of the shortest displacement from the starting point A to point the final position C is given by:

`AC=√((-41.25)^2+(11.85)^2)\ m= 42.94\ m`

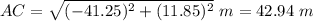
Part (2):

As the vector AC is coordinates lie in the third quadrant of the cartesian vector plane whose angle with the west will be positive in the north direction.

The angle of the shortest line connecting the starting point and the final position measured north of west is given by:

`\theta = \tan^(-1)((11.85)/(41.27))\\\Rightarrow \theta = 16.02^\circ`