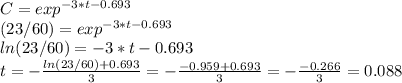Question

A tank initially contains 60 gallons of brine, with 30 pounds of salt in solution. Pure water runs into the tank at 3 gallons per minute and the well-stirred solution runs out at the same rate. How long will it be until there are 23 pounds of salt in the tank? Answer: the amount of time until 23 pounds of salt remain in the tank is minutes.

Answer 1

the amount of time until 23 pounds of salt remain in the tank is 0.088 minutes.

Explanation:

The variation of the concentration of salt can be expressed as:

`(dC)/(dt)=Ci*Qi-Co*Qo`

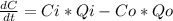
being

C1: the concentration of salt in the inflow

Qi: the flow entering the tank

C2: the concentration leaving the tank (the same concentration that is in every part of the tank at that moment)

Qo: the flow going out of the tank.

With no salt in the inflow (C1=0), the equation can be reduced to

`(dC)/(dt)=-Co*Qo`

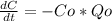
Rearranging the equation, it becomes

`(dC)/(C)=-Qo*dt`

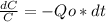
Integrating both sides

`\int(dC)/(C)=\int-Qo*dt\\ln(\abs{C})+x1=-Qo*t+x2\\ln(\abs{C})=-Qo*t+x\\C=exp^(-Qo*t+x)`

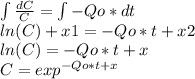
It is known that the concentration at t=0 is 30 pounds in 60 gallons, so C(0) is 0.5 pounds/gallon.

`C(0)=exp^(-Qo*0+x)=0.5\\exp^(x) =0.5\\x=ln(0.5)=-0.693\\`

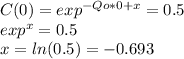
The final equation for the concentration of salt at any given time is

`C=exp^(-3*t-0.693)`

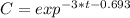
To answer how long it will be until there are 23 pounds of salt in the tank, we can use the last equation:

`C=exp^(-3*t-0.693)\\(23/60)=exp^(-3*t-0.693)\\ln(23/60)=-3*t-0.693\\t=-(ln(23/60)+0.693)/(3)=-(-0.959+0.693)/(3)=  -(-0.266)/(3)=0.088`