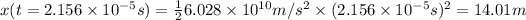Question

A proton accelarates from rest in a unifrom electric field of 630 N/C. At some later time, it's speed is 1.3 * 10^6 m/s. a) Find the magnitude of the acceleration of the proton. b) How long does it take the proton to reach this speed? c) How far has it moved in that interval?

Answer 1

a) 6.028*10^10 m/s^2

b)2.156*10^-5 s

c)14.01 m

Step-by-step explanation:

Hello!

I will not consider relativistic efects since the velocity of the proton is 1% of the velocity of ligth.

In order to find the acceleration we need to calculate first the force, this is done by multiplying the electric field times the charge of the proton (1e=1.6*10^-19)

`ma=F=630*1.6*10^(-19)N`

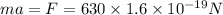
Since the mass of the proton is 1.6726219 × 10^-27 kilograms

The acceleration it suffers due to the electric field is:

`a = 6.028 *10^(10)m/s^(2)`

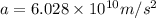
Since the proton accelerates from rest, the velocity as a function of time is given by:

`v = at`

So

`t=(1.3*10^(6)m/s)/(6.028 *10^(10)m/s^(2))=2.156*10^(-5)s`

Finally, the length traveled by the proton in that interval is given by:

`x(t=2.156*10^(-5)s)=(1)/(2) 6.028 *10^(10)m/s^(2)*(2.156*10^(-5)s)^(2)=14.01 m`