Question

A quadratic function is a function of the form y=ax^2+bx+c where a, b, and c are constants. Given any 3 points in the plane, there is exactly one quadratic function whose graph contains these points. Find the quadratic function whose graph contains the points (0, -2), (-5, -17), and (3, -17). Enter the equation below. Function: y = 0

Answer 1

The quadratic function whose graph contains these points is
`y=-x^(2)-2x-2`

Explanation:

We know that a quadratic function is a function of the form
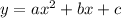`y=ax^(2)+bx+c`. The first step is use the 3 points given to write 3 equations to find the values of the constants a,b, and c.

Substitute the points (0,-2), (-5,-17), and (3,-17) into the general form of a quadratic function.

`-2=a*0^(2)+b*0+c\\c=-2`

`-17=a*-5^(2)+b*-5+c\\c=-25a+5b-17`

`-17=a*3^(2)+b*3+c\\ c=-9a-3b-17`

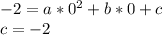
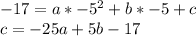
We can solve these system of equations by substitution

• Substitute
  `c=-9a-3b-17`

`-9a-3b-17=25a+5b-17\\-9a-3b-17=-2`

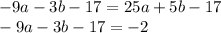
• Isolate a for the first equation

`-9a-3b-17=-25a+5b-17\\a=(b)/(2)`

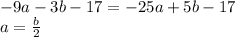
• Substitute
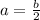  `a=(b)/(2)` into the second equation

`-9\left(-(b)/(2)\right)-3b-17=-2`

• Find the value of b

`-9\left(-(4b)/(17)\right)-3b-17=-2\\ b=-2`

• Find the value of a

`a=(b)/(2)\\  a=-1`

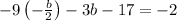
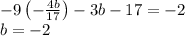
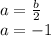
The solutions to the system of equations are:

b=-2,a=-1,c=-2

So the quadratic function whose graph contains these points is

`y=-x^(2)-2x-2`

As you can corroborate with the graph of this function.