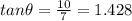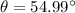Answer:12.206 cm,
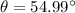
Step-by-step explanation:
Given
Insect walks 15 cm to the right
so its position vector is

Now it moves 10 cm up so its new position vector
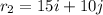
Now it moves 8 cm left so its final position vector is
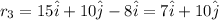
so its displacement is given by
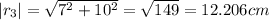
For direction, let \theta is the angle made by its position vector with x axis