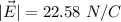Question

What is the magnitude (in N/C) and direction of an electric field that exerts a 3.50 ✕ 10−5 N upward force on a −1.55 µC charge?

Answer 1

The magnitude of electric field is 22.58 N/C

Solution:

Given:

Force exerted in upward direction,
`\vec{F_(up)} = 3.50* 10^(- 5) N`

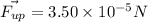
Charge, Q =
`- 1.55\micro C = - 1.55* 10^(- 6) C`

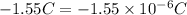
Now, we know by Coulomb's law,

Also,

Electric field,

Thus from these two relations, we can deduce:

F = QE

Therefore, in the question:

`\vec{E} = (\vec F_(up))/(Q)`

`\vec{E} = (3.50* 10^(- 5))/(- 1.55* 10^(- 6))`

`\vec{E} = - 22.58 N/C`

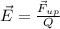
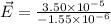
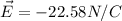
Here, the negative side is indicative of the Electric field acting in the opposite direction, i.e., downward direction.

The magnitude of the electric field is:

`|\vec{E}| = 22.58\ N/C`