Explanation:
To prove this we can use the definition of a sequence converging to its limit, in terms of epsilon:
The sequence
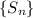 converges to
converges to

if and only if
for every
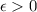 there exists
there exists
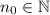 such that
such that
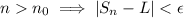
if and only if
for every
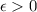 there exists
there exists
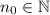 such that
such that
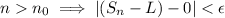
if and only if
the sequence
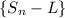 converges to 0.
converges to 0.