Question

An airplane is heading due south at a speed of 690 km/h . A) If a wind begins blowing from the southwest at a speed of 90 km/h (average), calculate the velocity (magnitude) of the plane relative to the ground.B) Calculate the velocity (direction) of the plane relative to the ground.C) Calculate how far from its intended position will it be after 11 min if the pilot takes no corrective action.

Answer 1

Answer:a) 629,5851 km/h in magnitude b)629,5851 km/h at 84,2 degrees from east pointing south direction or in vector form 626,6396 km/h south + 63,6396km/h east. c) 16,5 km NE of the desired position

Step-by-step explanation:

Since the plane is flying south at 690 km/h and the wind is blowing at assumed constant speed of 90 km/h from SW, we get a triangle relation where

see fig 1

Then we can decompose those 90 km/h into vectors, one north and one east, both of the same magnitude, since the angle is 45 degrees with respect to the east, that is direction norhteast or NE, then

90 km/h NE= 63,6396 km/h north + 63,6396 km/h east,

this because we have an isosceles triangle, then the cathetus length is

hypotenuse/
`√(2)`

using Pythagoras, here the hypotenuse is 90, then the cathetus are of length

90/
`√(2)` km/h= 63,6396 km/h.

Now the total speed of the plane is

690km/h south + 63,6396 km/h north +63,6396 km/h east,

this is 626,3604 km/h south + 63,6396 km/h east, here north is as if we had -south.

then using again Pythagoras we get the magnitude of the total speed it is

`√(626,3604 ^2+63,6396^2) km/h=629,5851km/h`,

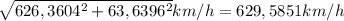the direction is calculated with respect to the south using trigonometry, we know the

sin x= cathetus opposed / hypotenuse,

then

x=
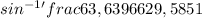`sin^(-1)'frac{63,6396}{629,5851}`=5,801 degrees from South as reference (0 degrees) in East direction or as usual 84,2 degrees from east pointing south or in vector form

626,6396 km/h south + 63,6396km/h east.

Finally since the detour is caused by the west speed component plus the slow down caused by the north component of the wind speed, we get

Xdetour{east}= 63,6396 km/h* (11 min* h)/(60 min)=11,6672 km=Xdetour{north} ,

since 11 min=11/60 hours=0.1833 hours.

Then the total detour from the expected position, the one it should have without the influence of the wind, we get

Xdetour=[/tex]\sqrt{2* 11,6672x^{2} }[/tex] = 16,5km at 45 degrees from east pointing north

The situation is sketched as follows see fig 2