Step-by-step explanation:
Charge,
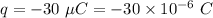
Electric force,
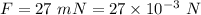
We need to find the magnitude and direction of electric field at that location. The relation between the electric field and electric force is given by :
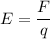

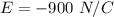
For a negative charge, the direction of electric field is inward. The direction of electric force and electric field is same. So, the direction of electric field in this case is in upward direction. Hence, this is the required solution.