Question

The atmospheric pressures at the top and the bottom of a building are read by a barometer to be 96.0 and 98.0 kPa. If the density of air is 1.0 kg/m^3, the height of the building is (a) 17 m (b) 20 m (c) 170 m (d) 204 m (e) 252 m e

Answer 1

Option d - 204 m

Explanation:

Given : The atmospheric pressures at the top and the bottom of a building are read by a barometer to be 96.0 and 98.0 kPa. If the density of air is 1.0 kg/m³.

To find : The height of the building ?

Solution :

We have given atmospheric pressures,

`P_{\text{top}}=96\ kPa`

`P_{\text{bottom}}=98\ kPa`

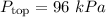
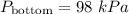
The density of air is 1.0 kg/m³ i.e.
`\rho_a=1\ kg/m^3`

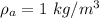
Atmospheric pressure reduces with altitude,

The height of the building is given by formula,

`H=(\triangle P)/(\rho_a* g)`

`H=\frac{P_{\text{bottom}}-P_{\text{top}}}{\rho_a* g}`

`H=((98-96)* 10^3)/(1* 9.8)`

`H=(2000)/(9.8)`

`H=204\ m`

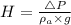
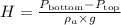
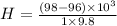
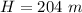
Therefore, Option d is correct.

The height of the building is 204 meter.