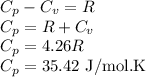Answer:
a)
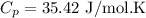
b)

Step-by-step explanation:
Given:
- Heat given to the gas,

- Initial volume of the gas,
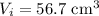
- Final volume of the gas,
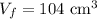
- Constant pressure of the gas,

- Number of moles of the gas,
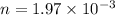
Let R be the gas constant which has value
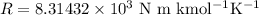
Work done in the process
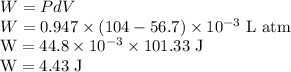
Now Using First Law of thermodynamics
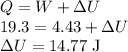
Let
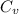 be the molar specific heat of the gas at constant volume given by
be the molar specific heat of the gas at constant volume given by
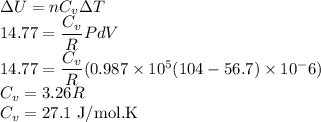
Also we know that
Let
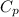 be the molar specific heat of the gas at constant pressure given by
be the molar specific heat of the gas at constant pressure given by