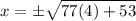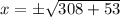Answer:
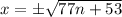
Explanation:
Given :
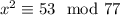
To find : All the square roots ?
Solution :
The primitive roots modulo is defined as
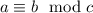
Where, a is reminder
b is dividend
c is divisor
Converting equivalent into equal,
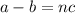
Applying in
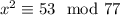 ,
,
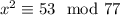
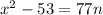
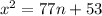
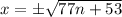
We have to find the possible value in which the x appear to be integer.
The possible value of n is 4.
As