Question

Consider the following equation: f(x) = 64-7x+ 4x^2

a) Take the deriivative and write out the equation, y= df/dx. Call this equation 1.

b)Let equation 2 be, y= f(x)/ x

c)Find the intersection of equation 1 and equation 2

Answer 1

Considering the equation f(x) = 64-7x+ 4x^2 this are the answers

a) Equation 1:

`y=8x-7`

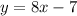
b) Equation 2:

`y=(64)/(x)-7+4x`

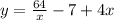
c) Intersection of Equation 1 and Equation 2:

The lines intersects in the points:

P(x,y)=(4,25) and P(x,y)=(-4,-39)

Explanation:

a) Drivate f(x) to find Equation 1:

y=f'(x)

y=0-7+8x

y=8x-7

b) Equation 2 is f(x)/x

y=f(x)/x

`y=(64-7x+4x^2)/(x)`

`y=(64)/(x)-7+4x`

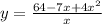
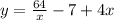
c) The intersection between the two equations is the only point that they have in common, this means that the points (x,y) satisfies both equations

To find it lets write the equations side by side

`\left \{ {{y=8x-7} \atop {y=(64)/(x)-7+4x}} \right.`

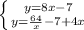
Given the fact that the y points are the same for both equations, you can replace the equation 1 into equation 2, this means, instead of write y, write equation 2:

`8x-7=(64)/(x)-7+4x`

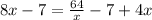
now you can solve this for x

`8x-4x-7+7=(64)/(x)\\4x=(64)/(x)\\4x^2=64`

`x^2=(64)/(4)\\x=√(16)\\ x=±4`

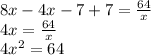
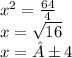
With the values of x, you can find the values of y by putting it into equation 1:

y=8*(+4)-7 and y=8*(-4)-7

y=25 and y=-39

Finally, the points where these two equations intersect are P(x,y)=(4,25) and P(x,y)=(-4,-39).