Answer:
In the step-by-step explanation, the verifications are made.
Explanation:
a)
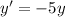
This one can be solved by the variable separation method
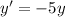
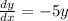
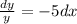
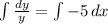
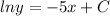

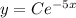
The value of C is the value of y when x = 0. If
 , then we have the following solution:
, then we have the following solution:
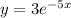
b)
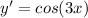
This one can also be solved by the variable separation method
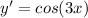
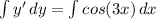
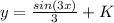
K is also the value of y, when x = 0. So, if
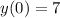 , we have the following solution.
, we have the following solution.
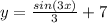
c)
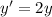
Another one that can be solved by the variable separation method
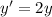
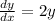

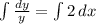
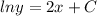
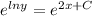
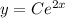
C is any real number depending on the initial conditions.
d)
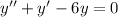
Here, the solution depends on the roots of the following equation:
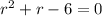
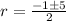
 or
or
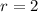 .
.
So the solution is
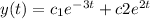
The values of
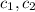 depends on the initial conditions.
depends on the initial conditions.
e)
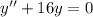
Again, we find the roots of the following equation:
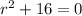
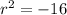
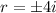
So we have the following solution

The values of
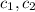 depends on the initial conditions.
depends on the initial conditions.