Question

For the following linear system, put the augmented coefficient matrix into reduced row-echelon form.

2x1 + 3x2 − x3 = 14

x1 + 2x2 + x3 = 4

5x1 + 9x2 + 2x3 = 7

1 0 -5 16

0 1 3 -6

0 0 0 -19

Incorrect

Answer 1

The reduced row-echelon form of the linear system is
`\left[\begin{array}{cccc}1&0&-5&0\\0&1&3&0\\0&0&0&1\end{array}\right]`

Explanation:

We will solve the original system of linear equations by performing a sequence of the following elementary row operations on the augmented matrix:

1. Interchange two rows
2. Multiply one row by a nonzero number
3. Add a multiple of one row to a different row

To find the reduced row-echelon form of this augmented matrix

`\left[\begin{array}{cccc}2&3&-1&14\\1&2&1&4\\5&9&2&7\end{array}\right]`

You need to follow these steps:

• Divide row 1 by 2
  `\left(R_1=(R_1)/(2)\right)`

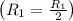
`\left[\begin{array}{cccc}1&3/2&-1/2&7\\1&2&1&4\\5&9&2&7\end{array}\right]`

• Subtract row 1 from row 2
  `\left(R_2=R_2-R_1\right)`

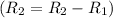
`\left[\begin{array}{cccc}1&3/2&-1/2&7\\0&1/2&3/2&-3\\5&9&2&7\end{array}\right]`

• Subtract row 1 multiplied by 5 from row 3
  `\left(R_3=R_3-\left(5\right)R_1\right)`

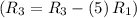
`\left[\begin{array}{cccc}1&3/2&-1/2&7\\0&1/2&3/2&-3\\0&3/9&9/2&-28\end{array}\right]`

• Subtract row 2 multiplied by 3 from row 1
  `\left(R_1=R_1-\left(3\right)R_2\right)`

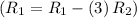
`\left[\begin{array}{cccc}1&0&-5&16\\0&1/2&3/2&-3\\0&3/9&9/2&-28\end{array}\right]`

• Subtract row 2 multiplied by 3 from row 3
  `\left(R_3=R_3-\left(3\right)R_2\right)`

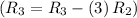
`\left[\begin{array}{cccc}1&0&-5&16\\0&1/2&3/2&-3\\0&0&0&-19\end{array}\right]`

• Multiply row 2 by 2
  `\left(R_2=\left(2\right)R_2\right)`

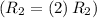
`\left[\begin{array}{cccc}1&0&-5&16\\0&2&3&-6\\0&0&0&-19\end{array}\right]`

• Divide row 3 by −19
  `\left(R_3=(R_3)/(-19)\right)`

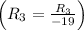
`\left[\begin{array}{cccc}1&0&-5&16\\0&2&3&-6\\0&0&0&1\end{array}\right]`

• Subtract row 3 multiplied by 16 from row 1
  `\left(R_1=R_1-\left(16\right)R_3\right)`

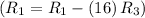
`\left[\begin{array}{cccc}1&0&-5&0\\0&1&3&-6\\0&0&0&1\end{array}\right]`

• Add row 3 multiplied by 6 to row 2
  `\left(R_2=R_2+\left(6\right)R_3\right)`

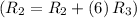
`\left[\begin{array}{cccc}1&0&-5&0\\0&1&3&0\\0&0&0&1\end{array}\right]`